> أَحَسِبَ ٱلنَّاسُ أَن يُتْرَكُوٓا۟ أَن يَقُولُوٓا۟ ءَامَنَّا وَهُمْ لَا يُفْتَنُونَ
QS. Al-‘Ankabūt: 2
Ayat ini bukan ekspresi keraguan, melainkan penegasan epistemik: keimanan tidak dibuktikan, tetapi diuji. Dalam logika formal, ini adalah distingsi antara aksioma dan konsekuensi operasional. Keimanan adalah titik tolak yang tidak tunduk pada pembuktian, melainkan untuk diterapkan secara konsisten dalam situasi nyata.
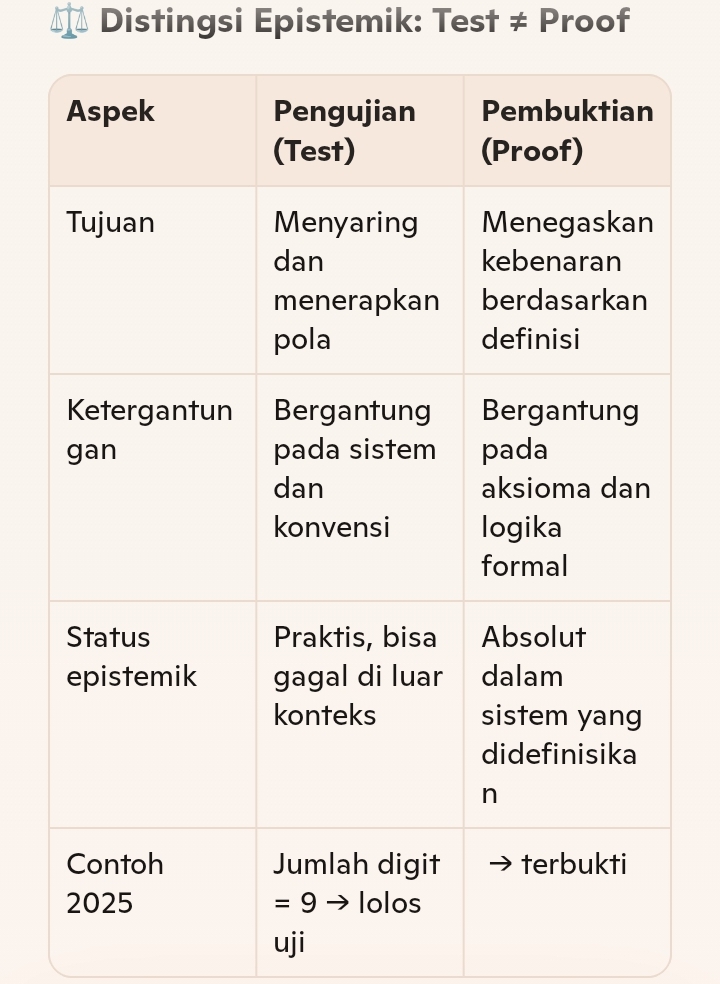
Untuk memperjelas distingsi ini, mari kita ambil contoh bilangan 2025 dan keterbagiannya dengan 9.
Pengujian: Apakah 2025 lolos tes digit 9?
Dalam sistem bilangan desimal, ada aturan praktis:
> Jika jumlah digit suatu bilangan habis dibagi 9, maka bilangan itu juga habis dibagi 9.
- Jumlah digit 2025:
2 + 0 + 2 + 5 = 9
- Karena 9 habis dibagi 9, maka 2025 lolos uji keterbagian.
Namun, ini bukan pembuktian. Ini adalah penerapan konsisten dari pola yang telah diuji dan digunakan secara luas. Ia bisa gagal di luar sistem desimal, atau jika definisi digit berubah. Maka, pengujian adalah alat praktis, bukan validasi mutlak.
Pembuktian: Apakah 2025 benar-benar habis dibagi 9?
Pembuktian menuntut definisi formal dan derivasi eksplisit:
- Kita nyatakan:
2025 = 9 x 225
- Karena hasilnya bilangan bulat tanpa sisa, maka secara definisi:
2025 terbukti habis dibagi 9.
Ini bukan penerapan pola, melainkan konfirmasi langsung terhadap definisi keterbagian:
> Bilangan a habis dibagi b jika terdapat bilangan bulat k sehingga a = b x k.
Penutup: Ujian adalah Konfirmasi Konsistensi, Bukan Validasi Kebenaran
QS.29:2 tidak sedang meminta manusia membuktikan keimanan mereka, melainkan menunjukkan apakah mereka konsisten menerapkannya dalam ujian. Sama seperti pengujian digit dalam aritmetika, ujian hidup tidak membatalkan aksioma, tetapi menguji apakah ia benar-benar diterapkan.
Dalam kerja epistemik, kita harus menjaga agar pengujian tidak disalahpahami sebagai pembuktian. Pengujian adalah bentuk komitmen terhadap konsistensi, bukan validasi terhadap kebenaran mutlak. Dan dalam dunia publik, membedakan keduanya adalah syarat kejujuran intelektual.
CATATAN:
Ketika kita mengatakan bahwa pengujian digit “bisa gagal di luar sistem desimal, atau jika definisi digit berubah,” kita sedang menyoroti bahwa pengujian keterbagian dengan menjumlahkan digit hanya berlaku dalam sistem tertentu dan dengan definisi tertentu. Mari kita uraikan dua aspek tersebut:
- Gagal di luar sistem desimal
Pengujian digit untuk keterbagian oleh 9 hanya berlaku dalam basis 10 (sistem desimal). Jika kita berpindah ke sistem bilangan lain, seperti basis 8 (oktal) atau basis 16 (heksadesimal), aturan ini tidak berlaku.
Contoh:
Ambil bilangan 2025 dalam sistem desimal. Kita tahu:
- Jumlah digit: 2 + 0 + 2 + 5 = 9
- Karena 9 habis dibagi 9, maka 2025 lolos uji keterbagian.
Namun, jika kita ubah 2025 ke sistem basis 8:
- 2025 desimal = 3741 dalam basis 8
- Jumlah digit: 3 + 7 + 4 + 1 = 15
Apakah 15 habis dibagi 9? Tidak. Tapi 2025 tetap habis dibagi 9 secara definisi.
Artinya: pengujian digit gagal di basis 8.
Karena aturan jumlah digit hanya berlaku dalam basis 10, ia tidak universal.
- Gagal jika definisi digit berubah
Dalam sistem desimal, “digit” berarti angka 0 sampai 9. Tapi jika kita mengubah definisi digit—misalnya, menyertakan digit sebagai representasi posisi atau menggunakan digit dalam sistem bilangan campuran—maka pengujian digit bisa kehilangan maknanya.
Contoh ekstrem:
Bayangkan sistem bilangan di mana digit bukan angka, tapi huruf yang mewakili nilai tertentu (misalnya, A = 1, B = 2, …, I = 9).
Jika kita menulis 2025 sebagai “B0B5” (mengganti 2 dengan B, 5 dengan E), maka menjumlahkan “digit” menjadi ambigu: apakah kita menjumlahkan nilai numeriknya, atau hanya menghitung simbol?
Jika definisi digit tidak konsisten, maka pengujian digit tidak bisa dilakukan secara operasional, karena kita tidak tahu apa yang sedang dijumlahkan.
Simpulan:
Pengujian digit adalah alat praktis yang bergantung pada sistem dan definisi. Ia bukan pembuktian, karena tidak universal dan bisa gagal jika konteks berubah. Maka, dalam epistemologi publik, kita harus berhati-hati: jangan menyamakan keberhasilan pengujian dengan validitas pembuktian.
Distingsi ini penting bukan hanya dalam matematika, tapi juga dalam kehidupan beriman dan berpikir jernih: aksioma tidak dibuktikan, tetapi diuji melalui penerapan konsisten dalam sistem yang telah didefinisikan.